How to Write a Polynomial in Standard Form With Two Variables Having the Same Exponent
Polynomials
A polynomial looks like this:
 |
| example of a polynomial this one has 3 terms |
Polynomial comes from poly- (meaning "many") and -nomial (in this case meaning "term") ... so it says "many terms"
Polynomials with one variable make nice smooth curves:

A polynomial can have:
that can be combined using addition, subtraction, multiplication and division ...
... except ...
... not division by a variable (so something like 2/x is right out)
So:
A polynomial can have constants, variables and exponents,
but never division by a variable.
Also they can have one or more terms, but not an infinite number of terms.
Polynomial or Not?

These are polynomials:
- 3x
- x − 2
- −6y2 − ( 7 9 )x
- 3xyz + 3xy2z − 0.1xz − 200y + 0.5
- 512v5 + 99w5
- 5
(Yes, "5" is a polynomial, one term is allowed, and it can be just a constant!)
These are not polynomials
- 3xy-2 is not, because the exponent is "-2" (exponents can only be 0,1,2,...)
- 2/(x+2) is not, because dividing by a variable is not allowed
- 1/x is not either
- √x is not, because the exponent is "½" (see fractional exponents)
But these are allowed:
- x/2 is allowed, because you can divide by a constant
- also 3x/8 for the same reason
- √2 is allowed, because it is a constant (= 1.4142...etc)
Monomial, Binomial, Trinomial
There are special names for polynomials with 1, 2 or 3 terms:

How do you remember the names? Think cycles! 
There is also quadrinomial (4 terms) and quintinomial (5 terms),
but those names are not often used.
Variables
Polynomials can have no variable at all
Example: 21 is a polynomial. It has just one term, which is a constant.
Or one variable
Example: x4 − 2x2 + x has three terms, but only one variable (x)
Or two or more variables
Example: xy4 − 5x2z has two terms, and three variables (x, y and z)
What is Special About Polynomials?
Because of the strict definition, polynomials are easy to work with.
For example we know that:
- If you add polynomials you get a polynomial
- If you multiply polynomials you get a polynomial
So you can do lots of additions and multiplications, and still have a polynomial as the result.
Also, polynomials of one variable are easy to graph, as they have smooth and continuous lines.
Example: x4−2x2+x
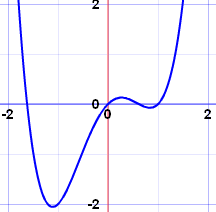 | See how nice and |
You can also divide polynomials (but the result may not be a polynomial).
Degree
The degree of a polynomial with only one variable is the largest exponent of that variable.
Example:
| 4x3 − x + 2 | The Degree is 3 (the largest exponent of x ) |
For more complicated cases, read Degree (of an Expression).
Standard Form
The Standard Form for writing a polynomial is to put the terms with the highest degree first.
Example: Put this in Standard Form: 3x2 − 7 + 4x3 + x6
The highest degree is 6, so that goes first, then 3, 2 and then the constant last:
x6 + 4x3 + 3x2 − 7
You don't have to use Standard Form, but it helps.
342, 343, 1095, 1096, 3182, 3183, 3184, 3185, 1097, 4002
How to Write a Polynomial in Standard Form With Two Variables Having the Same Exponent
Source: https://www.mathsisfun.com/algebra/polynomials.html
0 Response to "How to Write a Polynomial in Standard Form With Two Variables Having the Same Exponent"
Post a Comment